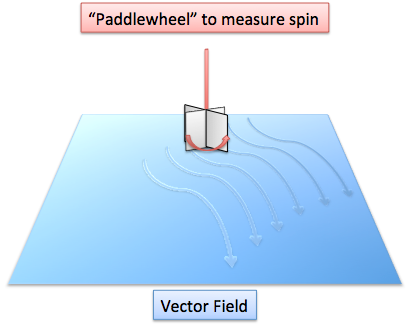
Vector Field Curl 3d
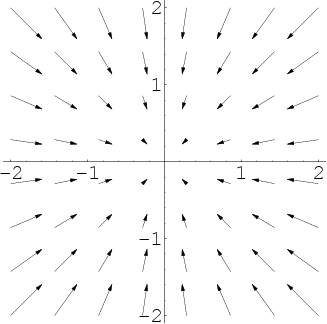
If f f is a conservative vector field then curl f 0 curl f 0.
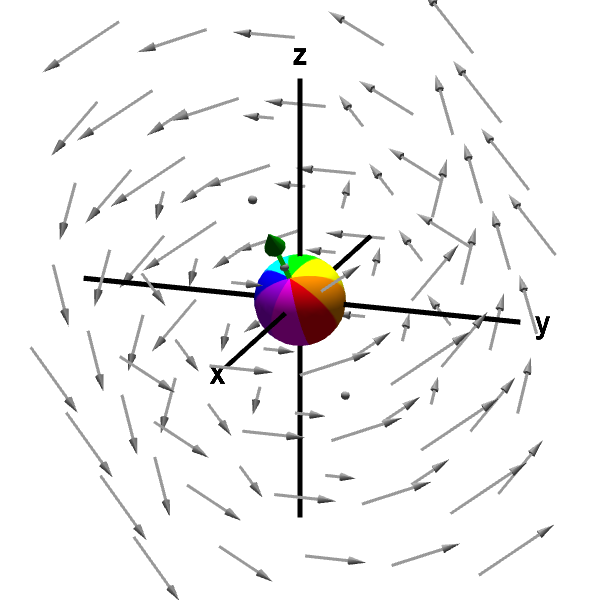
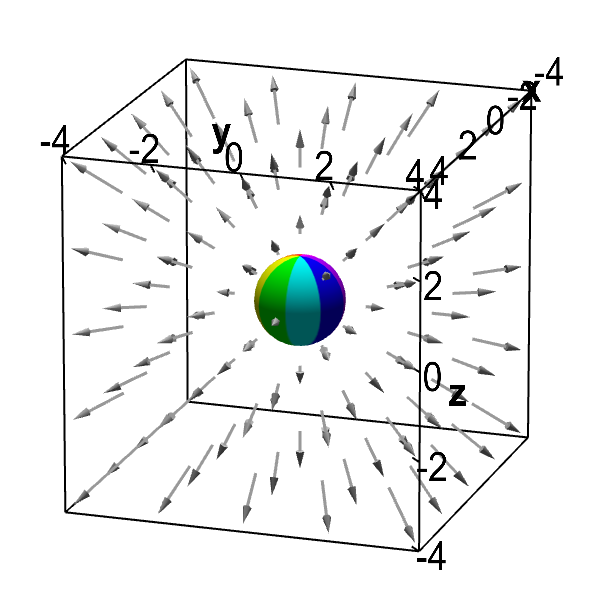
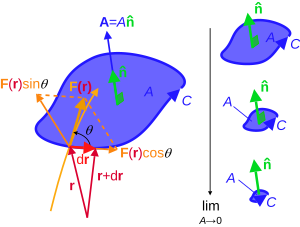
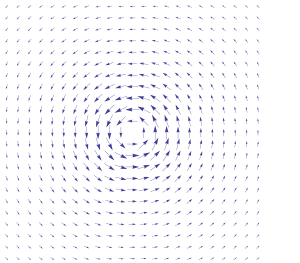
Vector field curl 3d. 0 energy points. The attributes of this vector length and direction characterize the rotation at that point. This is a direct result of what it means to be a conservative vector field and the previous fact. 3d vector field example.
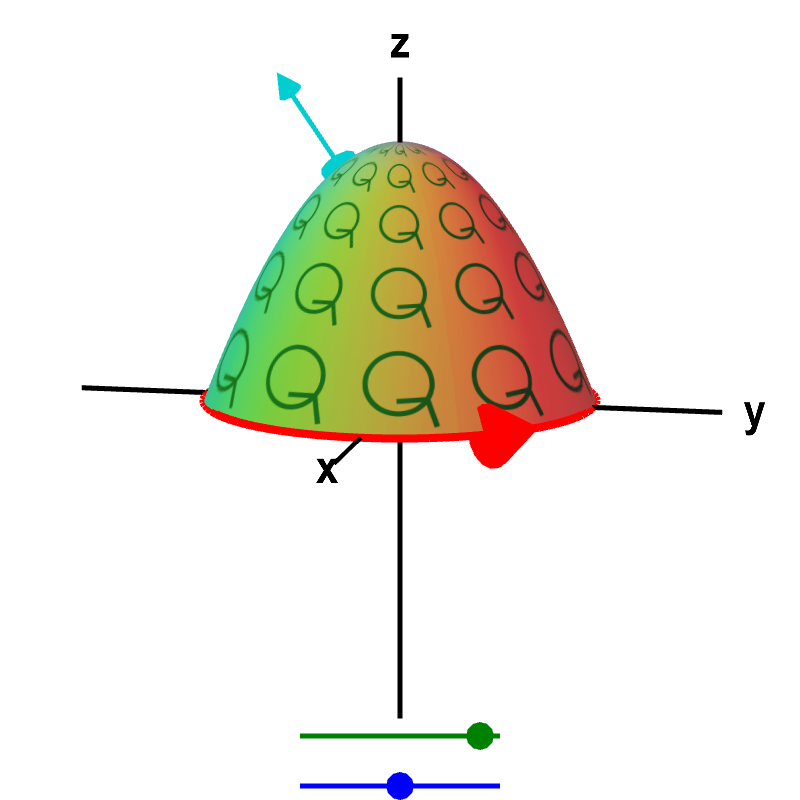
See an example of how you can start to understand how the formula for a three dimensional vector field relates to the way it looks. So the partial of q with respect to x minus the partial derivative of that first component with respect to y. You can also input your own by scrolling to the bottom of that menu and selecting. Integral is of the vector field f x y z x 2 z e y y 3 x z e y z 4 x e y.
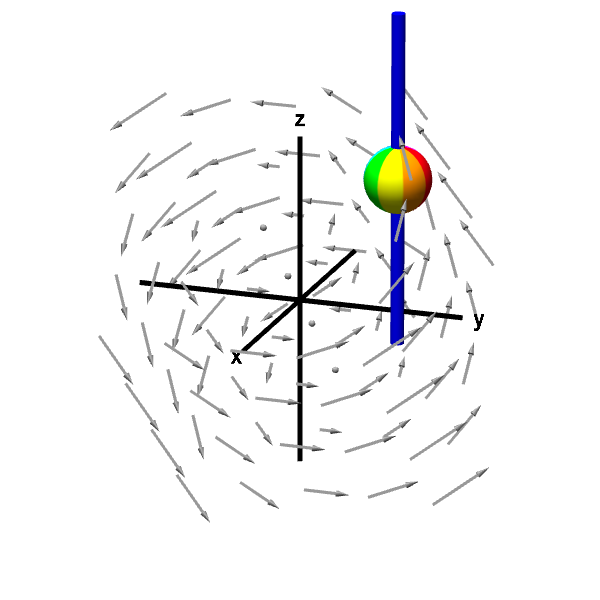
Three d curl is the kind of thing that you take with regards to a three dimensional vector field. You can select from a number of vector fields and see how particles move if it is treated as either a velocity or a force field. Math multivariable calculus thinking about multivariable functions. So something that takes in a three dimensional point as its input and then it s going to output a three dimensional vector.
This is the currently selected item. The partial derivatives of f are. 3d vector fields introduction. It s common to write the component functions as p q and r.
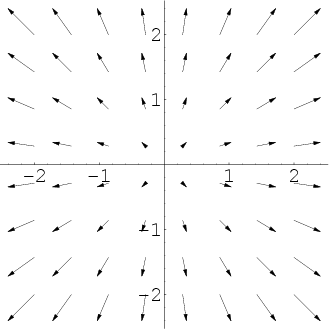
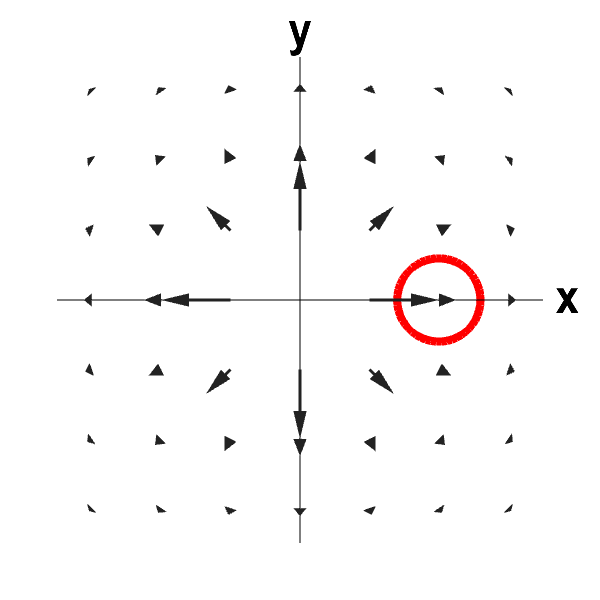
The vector field f defined on r 3 which is simply connected. You see if this whole thing if we give names to the two different component functions as p and q then the curl the two d curl of this guy two d curl of the vector field v has a function of x and y what it equals is the partial derivative of that second component with respect to x. This is easy enough to check by plugging into the definition of the derivative so we ll leave it to you to check. At every point in the field the curl of that point is represented by a vector.
The menu in the upper right has a variety of different fields to choose from. The third snapshot shows a conservative vector field that has a constant curl equal to zero at every point. This java applet demonstrates various properties of vector fields. In vector calculus the curl is a vector operator that describes the infinitesimal rotation of a vector field in three dimensional euclidean space.